ChoCG: Lid-driven cavity
This example uses ChoCG in Inciter to compute the stationary viscous constant-density (incompressible) laminar flow field in a driven by a shearing velocity on one side. The numerical solution is compared to those published in [1].
Problem setup
Since the problem is essentially 2D, the computational domain is a brick with a single element thickness in the Z dimension. Solid walls with no-slip/no-penetration boundary conditions are prescribed on 3 faces of the domain and a constant shear-velocity is applied on the Y extreme. Free-slip (symmetry) conditions are prescribed at faces with Z normals. The initial conditions prescribe a quiescent state with . The boundaries at walls prescribe no-slip/no-penetration with . The shear velocity on the top is enforced using a Dirichlet condition as . The Reynolds number , is defined basd on the dynamic viscosity , the fluid density , the charactieristic length , and the imposed shear velocity of . We used different meshes depending on the Reynolds number, listed below.
| Mesh | Points | Tetrahedra | h |
|---|---|---|---|
| 32x32 | 2,178 | 6,144 | 0.036232 |
| 128x128 | 33,282 | 98,304 | 0.015841 |
| 256x256 | 132,098 | 393,216 | 0.012821 |
Here h is the average edge length. The mesh labeled '128x128' is depicted below.
 Surface mesh for computing the lid-driven cavity flow with , nelem=98K, npoin=33K.
Surface mesh for computing the lid-driven cavity flow with , nelem=98K, npoin=33K.Code revision to reproduce
To reproduce the results below, use code revision ece4f40 and the control file below.
Control file
-- vim: filetype=lua: print "Lid-driven cavity" -- mesh: ldc90_32x32_tet.exo Re=100 -- ldc90_128x128_tet.exo Re=1000 -- ldc90_256x256_tet.exo Re=5000 term = 100.0 ttyi = 10 cfl = 0.7 solver = "chocg" flux = "damp4" rk = 4 part = "rcb" Re = 1000.0 mat = { dyn_viscosity = 1.0/Re } momentum = { iter = 50, tol = 1.0e-3, pc = "jacobi" } pressure = { iter = 1000, tol = 1.0e-3, pc = "jacobi", hydrostat = 0 } ic = { velocity = { 0.0, 0.0, 0.0 } } bc_noslip = { sideset = { 6 } } bc_sym = { sideset = { 3 } } bc_dir = { { 4, 2, 2, 2 } } bc_dirval = { { 4, 1.0, 0.0, 0.0 } } fieldout = { iter = 1000 } diag = { iter = 1, format = "scientific", precision = 12 }
Run on 32 CPUs
./charmrun +p32 Main/inciter -i ldc90_128x128_tet.exo -c ldch_chocg.q
Visualization
ParaView can be used for interactive visualization of the numerically computed 3D fields as
paraview out.e-s.0.32.0The converged velocity field distribution at on the domain surface surface is depicted below.
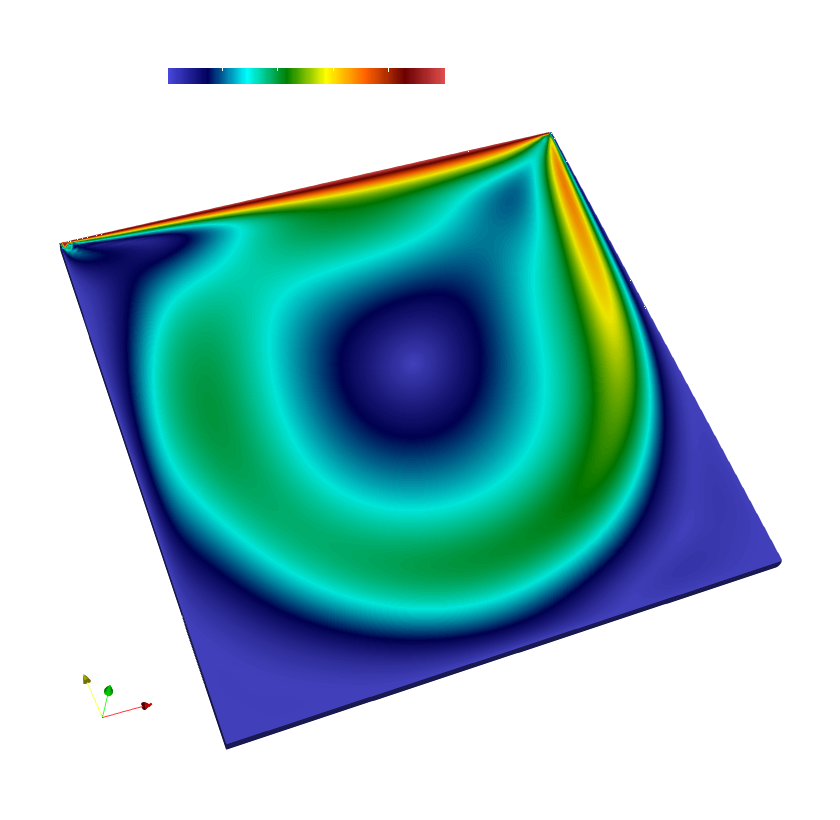
Numerical solution
Plotted below are the computed velocity profiles sampled in the middle of the domain along lines in the X and Y directions, obtained after the solution has converged to a stationary state. The numerical solution is compared to those in [1].
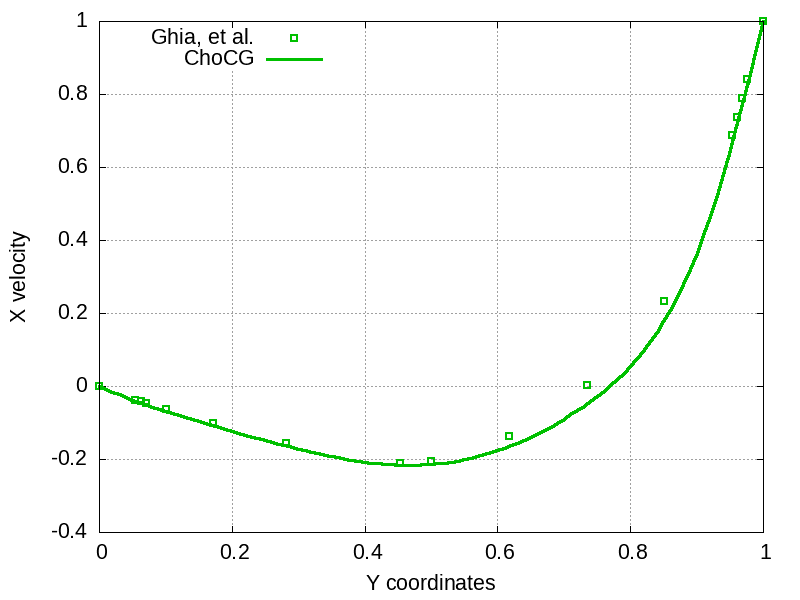
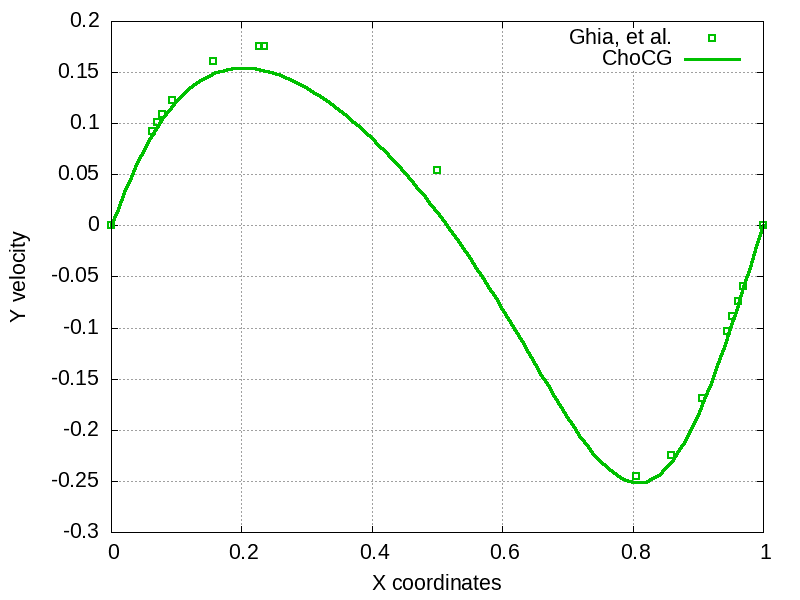
References
- U. Ghia, K.N. Ghia, and C.T. Shin, High-Re Solutions of Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method, Journal of Computational Physics, 48(3), 387-411, 1982.