V&V » ChoCG: Dispersion from a point source in shear flow

This example uses ChoCG in Inciter to compute a problem featuring advection, shear, and diffusion of a passive scalar. Since the analytic solution is known as a function of time, numerical errors can be estimated. This enables quantifying the accuracy of the numerical method as well as verifying the correctness of the implementation.

Equations solved

In this example we numerically solve the linear advection equation of a passive scalar, denoted by $c$ , representing the normalized concentration of a pollutant released from a concentrated source, coupled to the Navier-Stokes equations governing viscous Newtonian constant-density flow, see also ChoCG, as

\[ \begin{split} \frac{\partial\mbox{\boldmath$v$}}{\partial t} + \mbox{\boldmath$v$}\cdot\nabla\mbox{\boldmath$v$} + \nabla p & = \nabla\mu\nabla\mbox{\boldmath$v$} \\ \frac{\partial\mbox{c}}{\partial t} + \mbox{\boldmath$v$}\cdot\nabla\mbox{c} & = D \nabla^2 c \\ \nabla\cdot\mbox{\boldmath$v$} & = 0 \end{split} \]

where $\mbox{\boldmath$v$}$ is the velocity vector, $p$ is the pressure, and both the pressure and the viscosity $\mu$ have been normalized by the (constant) density. Here $D$ is the scalar diffusivity.

Problem setup

This problem and its analytical solution was presented by Carter and Obuko [1] with further related discussion in [2]. For the simple steady two dimensional uni-directional flow, with velocity $u_0$ along the $x$ axis, shear $\lambda = \mathrm{d}u/\mathrm{d}y$ and constant diffusion coefficient, $D$ , the governing equation is

\[ \frac{\partial c}{\partial t}+\left(u_0+\lambda y\right)\frac{\partial c}{\partial x}=D\left(\frac{\partial^2c}{\partial x^2}+\frac{\partial^2c}{\partial y^2}\right)\quad\quad\left(-\infty<x<\infty\right), \]

subject to initial conditions

\[ \begin{split} c(x,y,0) & = c_0(x,y) \\ c(x,y,t) & \rightarrow 0\enskip\mathrm{as}\enskip|x|\enskip\mathrm{or}\enskip|y|\rightarrow\infty \end{split} \]

When the initial condition is a point source of mass $M$ at $(x = x_0 ,y = y_0, t = 0)$ , the solution is

\[ c\left(x,y,t\right)=\frac{M}{4\pi t\sqrt{1+\lambda^2t^2/12}}\exp\left(-\frac{\left(x-x_0-u_0t-\lambda yt/2\right)^2}{4\pi Dt\left(1+\lambda^2t^2/12\right)}-\frac{y^2}{4Dt}\right) \]

To allow the numerical solution to be based on a finite source size, the calculation is started at time $t=t_0$ with a concentration distribution given by the above analytic solution using $M=4\pi t_0\sqrt{1+\lambda^2t_0^2/12}$ , i.e., the initial concentration peak is unity. The problem is solved on a 3D rectangular domain with a few cells in the $Z$ dimension and extents $(x\in[0,24000];y\in[-3400,3400]$ with $x_0=y_0=0$ , $t_0=2400$ , $u_0=0.5$ , $\lambda=1.0\times10^4$ , and $D=50.0$ .

The initial conditions are sampled from the analytic solutions above. We set inhomogeneous Dirichlet boundary conditions for all variables on the sides of the domain with normals in the $x$ or $y$ directions, sampling their analytic solutions. On the sides with normals in the $z$ direction, the flow variables are sampled from their analytic solutions, while for the scalar, homogeneous Neumann conditions are enforced.

Image Coarse surface mesh for computing the shear-diffusion test problem, nelem=15K, npoin=3K.

Code revision to reproduce

To reproduce the results below, use code revision 917090c and the control file below.

Control file

-- vim: filetype=lua:

print "2D shear-diffusion"

-- mesh: shear_15K.exo
--       shear_124K.exo

t0 = 2400.0
term = 9600.0
ttyi = 1

cfl = 0.4

solver = "chocg"
flux = "damp4"
rk = 4

part = "rcb"

problem = {
  name = "sheardiff",
  p0 = 0.5,             -- x translation velocity (u_0)
  alpha = 1.0e-4        -- y shear velocity (lambda)
}

mat = {
  dyn_diffusivity = 50.0
}

pressure = {
  iter = 1,
  tol = 1.0e-3,
  pc = "jacobi",
  hydrostat = 0
}

bc_dir = {
  { 1, 1, 1, 1, 1 },
  { 2, 1, 1, 1, 0 }
}

fieldout = {
  iter = 100
}

diag = {
  iter = 1,
  format = "scientific",
  precision = 12
}

Run using on 32 CPUs

./charmrun +p32 Main/inciter -i shear_124K.exo -c sheardiff_chocg.q

Visualization

ParaView can be used for interactive visualization of the numerically computed fields as

paraview out.e-s.0.32.0

The scalar field is displayed at the initial and final times below.

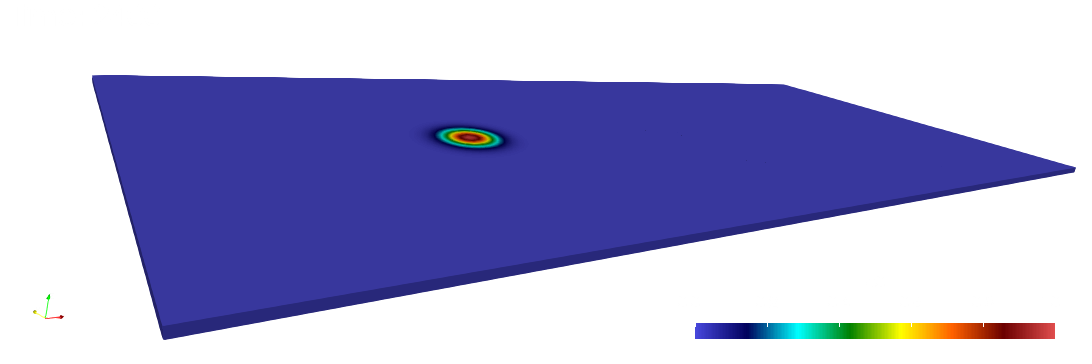
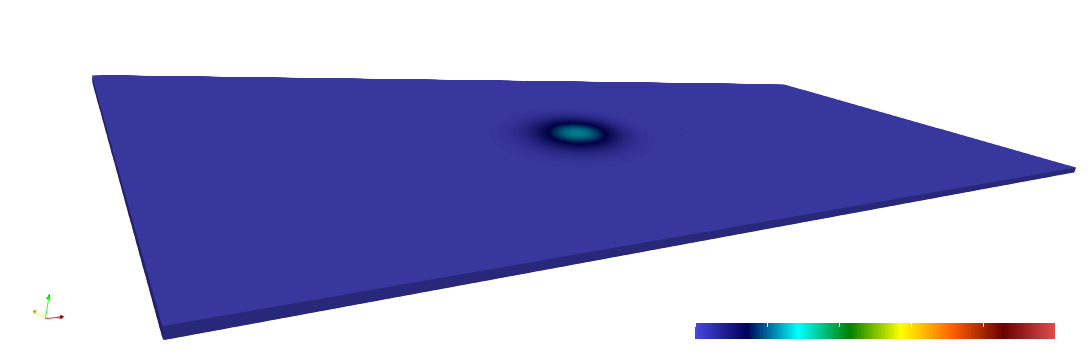
Image Image

Numerical solutions and errors

To estimate the order of convergence, the numerical solution was computed using two different meshes, whose properties of are tabulated below.

MeshPointsTetrahedrah
13,1349,123640.99
224,99274,156218.97

Here h is the average edge length. The L1 and L2 errors are computed as

\[ \begin{split} \left| \left| \varepsilon \right| \right|_1 & = \frac{\sum_{i=1}^n V^i \left| \hat{c}^i - c^i \right|} {\sum_{i=1}^n V^i} \\ \left| \left| \varepsilon \right| \right|_2 & = \left[\frac{\sum_{i=1}^n V^i \left( \hat{c}^i - c^i \right)^2} {\sum_{i=1}^n V^i}\right]^{1/2} \end{split} \]

where $n$ is the total number of points in the whole domain, $\hat{c}^i$ and $c^i$ are the exact and computed scalar concentrations at mesh point $i$ , and $V^i$ denotes the volume associated to mesh point $i$ . The table below displays the numerical errors for the two meshes and the estimated order of convergence, computed by

\[ p = \frac{ \log \left| \left| \varepsilon \right| \right|^{m+1} - \log \left| \left| \varepsilon \right| \right|^m}{ \log h^{m+1} - \log h^m} \]

where $m$ is a mesh index.

MeshhL1(err)L2(err)
1640.996.448e-043.674e-03
2218.975.734e-053.289e-04
p2.2532.247

References

  1. H. Carter, A. Okubo, A study of the physical processes of movement and dispersion in the Cape Kennedy area, Chesapeake Bay Inst. Ref. 65-2, Johns Hopkins Univ., 1965.
  2. A. Okubo, M. Karweit, Diffusion from a continuous source in a uniform shear flow, Limm. and Oceano. 14(4) 514-520., 1969.