ChoCG: Viscous flow past a sphere
This example uses ChoCG in Inciter to compute the viscous constant-density (incompressible) flow past a sphere. The goal is to compute the drag on the sphere at various Reynolds numbers which can be compared to experimental data allowing validation of the numerical method and its software implementation.
Problem setup
Due to the spatial symmetry of the problem, only half of the sphere is represented in the computational domain. We use a coarser and a finer mesh, listed below, for lower and higher Reynolds numbers, respectively.
| Mesh | Points | Tetrahedra | h |
|---|---|---|---|
| 128K | 22,530 | 119,390 | 1.135276 |
| 960K | 165,632 | 925,005 | 0.582934 |
As an example, the finer surface mesh is depicted below. The initial conditions prescribe the homogeneous free-stream velocity of . The pressure is set to zero at the outflow and the velocity is set to at the inflow. No-slip/no-penetration boundary conditions are applied on the sphere surface while free-slip conditions are enforced on the symmetry half-plane. Free-stream conditions are prescribed on the rest of the boundaries far from the sphere.
 Surface mesh for computing viscous flow past a sphere.
Surface mesh for computing viscous flow past a sphere.Code revision to reproduce
To reproduce the results below, use code revision 3b9b55e and the control file below.
Control file
-- vim: filetype=lua: print "Viscous half sphere" -- mesh: half_viscous_sphere_128K.exo -- half_viscous_sphere_960K.exo -- sphere diam = 1.0 -- plot "diag" u 2:8 t "L2(dp)" w l lw 2, "" u 2:9 t "L2(du)" w l lw 2, "" u 2:10 t "L2(dv)" w l lw 2, "" u 2:11 t "L2(dw)" w l lw 2 -- plot "out.int" u 2:(-$4*8.0/pi*2.0) w l lw 2 t "Cd" term = 20.0 ttyi = 10 cfl = 0.7 solver = "chocg" flux = "damp4" rk = 4 part = "phg" zoltan_params = { "PHG_COARSENING_METHOD", "AGG", "PHG_COARSEPARTITION_METHOD", "GREEDY", "PHG_REFINEMENT_QUALITY", "5", --"PHG_CUT_OBJECTIVE", "HYPEREDGES" "PHG_CUT_OBJECTIVE", "CONNECTIVITY" } pressure = { iter = 300, tol = 1.0e-3, pc = "jacobi", bc_dir = { { 3, 1 } } } Re = 300.0 mat = { dyn_viscosity = 1.0/Re } ic = { velocity = { 1.0, 0.0, 0.0 } } bc_dir = { { 2, 1, 1, 1 }, -- inflow { 5, 1, 1, 1 } -- farfield } bc_noslip = { sideset = { 1 } } bc_sym = { sideset = { 4 } } fieldout = { iter = 1000, sideset = { 1, 4 } } integout = { iter = 10, sideset = { 1 }, integrals = { "force" } } diag = { iter = 10, format = "scientific", precision = 12 }
Run on 128 CPU cores in Charm++'s non-SMP mode using SLURM
srun --nodes=1 --ntasks-per-node=128 Main/inciter -c sphere_chocg_viscous_half.q -i half_viscous_sphere_960K.exo -r 100000 -l 100000
Visualization and numerical results
ParaView can be used for interactive visualization of the numerically computed 3D fields as
paraview out.e-s.0.128.0Results only on the sphere and symmetry half-plane surfaces can be visualized by first stitching the partitioned surface output files into single surface output files, followed by invoking paraview loading both stitched surface exo files:
meshconv -i out-surf.1.e-s.0.128.% -o out-surf.1.exo meshconv -i out-surf.4.e-s.0.128.% -o out-surf.4.exo paraview --data="out-surf.1.exo;out-surf.4.exo"
Example pressure and velocity magnitude distributions along the symmetry and sphere surfaces at are shown in the figures below. Here the Reynolds number is defined as , based on the free-stream velocity, , sphere diameter, , fluid density, , and dynamic viscosity, .
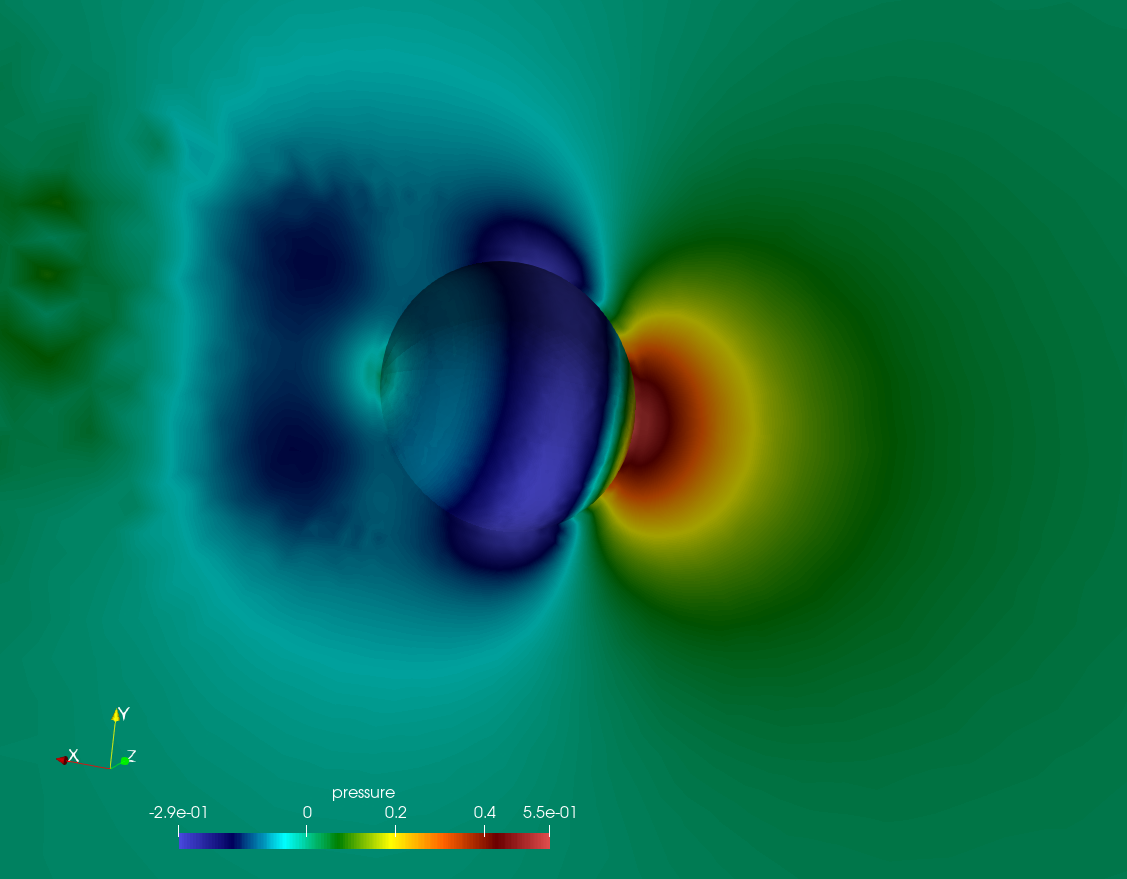
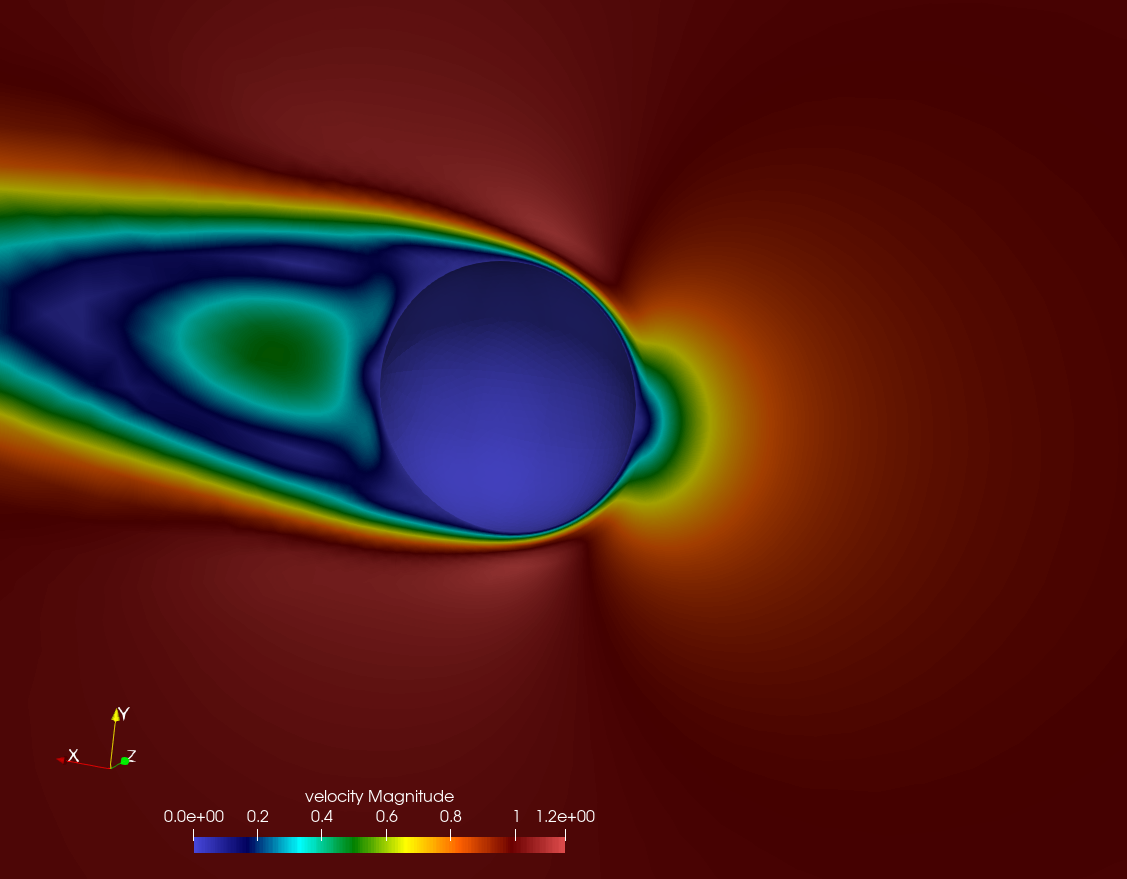
Drag
Repeatedly performing the above simulation with different Reynolds numbers and computing the force the fluid exerts on the sphere allow numerically estimating the drag coefficient which can be compared to experimental data in [1] and thus validating the solver implementation. The force is defined by the integral
Here is the wall normal, is the sphere surface, is the pressure, is the velocity vector, while denotes the Kronecker delta. The drag coefficient is defined based on the streamwise force, ,
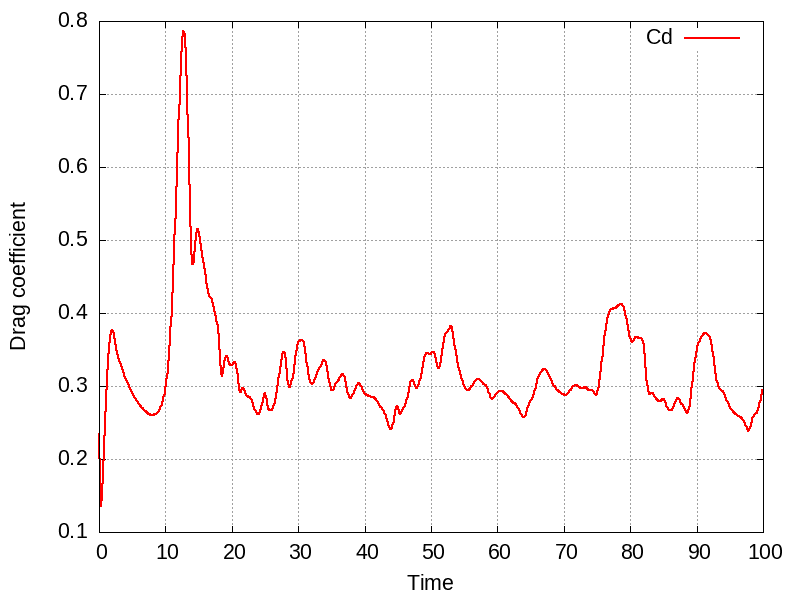
where is the surface of the sphere in the streamwise direction [1]. Plotted below are example time-evolutions of the computed drag coefficient for and , respectively, depicting stationary and non-stationary flows.
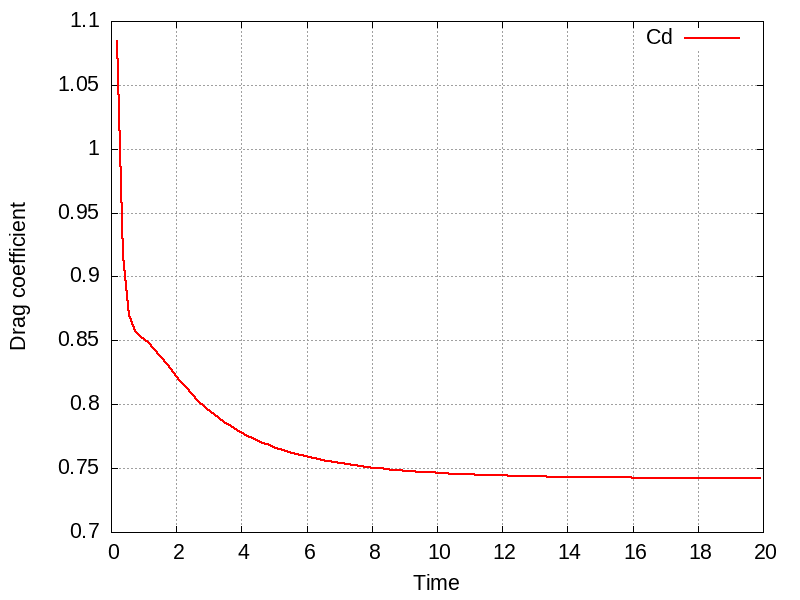
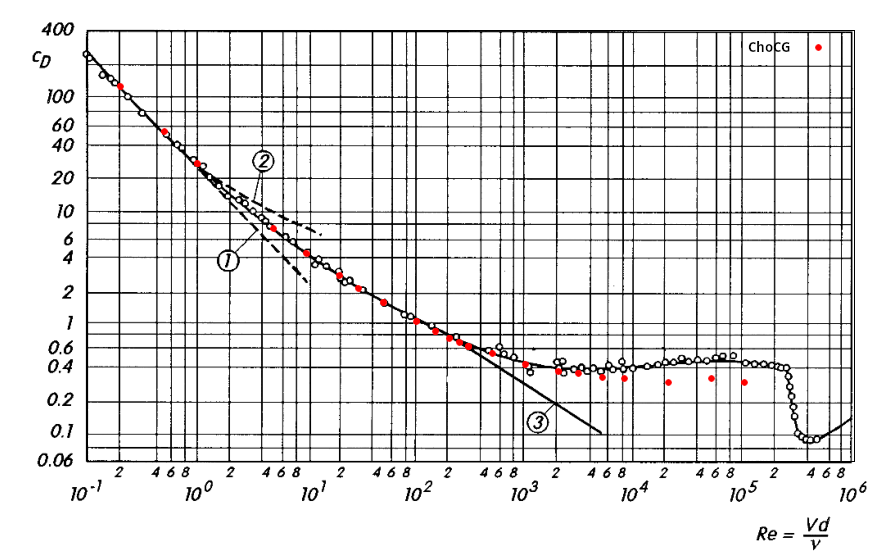
The drag coefficient computed by ChoCG at different Reynolds numbers are overlaid on Fig.1.19 taken from [1] below, showing good agreement with theory and experimental data at all Reynolds numbers computed.

References
- H. Schlichting, and K. Gersten, Boundary-Layer Theory, Springer, 9th edition, 2017.