RieCG: Sedov blast
This example uses RieCG in Inciter to compute the Sedov problem [1], widely used in shock hydrodynamics to test the ability of numerical methods to maintain symmetry. In this problem, a source of energy is defined to produce a shock in a single computational cell at the origin at t=0. The solution is a spherically spreading wave starting from a single point. The semi-analytic solution is known, therefore it can be used to verify the accuracy of the numerical method and the correctness of the software implementation.
Problem setup
We compute the solution in 3D using a simulation domain that is an octant of a sphere, centered around the point {0,0,0}, with increasing mesh resolutions.
The initial conditions are
where and are initial values of the internal energy and pressure respectively, that depend on the size of the control volume at the center of the sphere. As the mesh size is decreased, these values are increased to maintain a constant total energy source. The characteristics of the meshes used are listed in the table below.
| Mesh | Points | Tetrahedra | h | e_s | p_s |
|---|---|---|---|---|---|
| 0 | 11,304 | 59,164 | 0.053 | 7.25e+3 | 4.86e+3 |
| 1 | 65,958 | 362,363 | 0.029 | 5.42e+4 | 3.63e+4 |
| 2 | 505,724 | 2,898,904 | 0.014 | 3.46e+5 | 2.32e+5 |
| 3 | 3,956,135 | 23,191,232 | 0.007 | 2.78e+6 | 1.85e+6 |
| 4 | 31,286,637 | 185,529,856 | 0.004 | 2.22e+7 | 1.48e+7 |
Here h is the average edge length. Along the flat faces of the sphere symmetry (free-slip) boundary conditions are applied.
Code revision to reproduce
To reproduce the results below, use code revision fadd412 and the control file below, and adjust for the mesh.
Control file
-- vim: filetype=lua: print "Sedov blast wave" term = 1.0 ttyi = 100 cfl = 0.5 part = "rcb" solver = "riecg" problem = { name = "sedov", -- p0 = 4.86e+3 -- sedov_coarse.exo, V(orig) = 8.50791e-06 -- p0 3.63e+4 -- sedov00.exo, V(orig) = 1.13809e-06 -- p0 2.32e+5 -- sedov01.exo, V(orig) = 1.78336e-07 p0 1.85e+6 -- sedov02.exo, V(orig) = 2.22920e-08 -- p0 14773333.33333 -- sedov02.exo+t0ref:u,V(orig) = 2.78650e-09 } mat = { spec_heat_ratio = 5/3 } bc_sym = { sideset = { 1, 2, 3 } } -- href = { -- t0 = true, -- init = { "uniform" } -- } diag = { iter = 10, format = "scientific" } fieldout = { iter = 1000 }
Run using mesh 3 on 32 CPUs
./charmrun +p32 Main/inciter -i sedov02.exo -c sedov.q -l 1000
Visualization
ParaView can be used for interactive visualization of the numerically computed fields as
paraview out.e-s.0.32.0The fluid density on the sphere octant surface using mesh 3 and its radial distributions using different mesh resolutions at t=1.0s are depicted below.
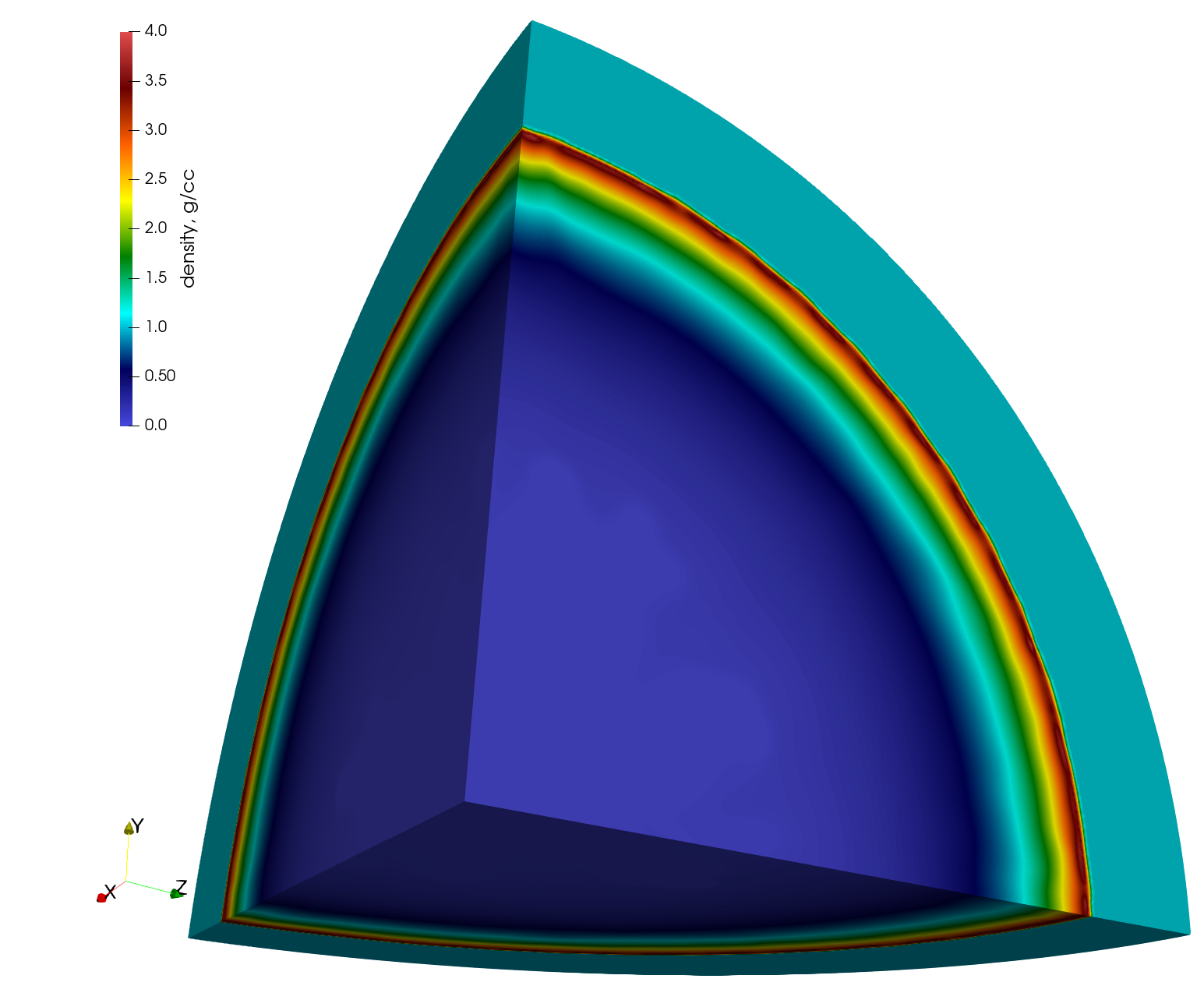
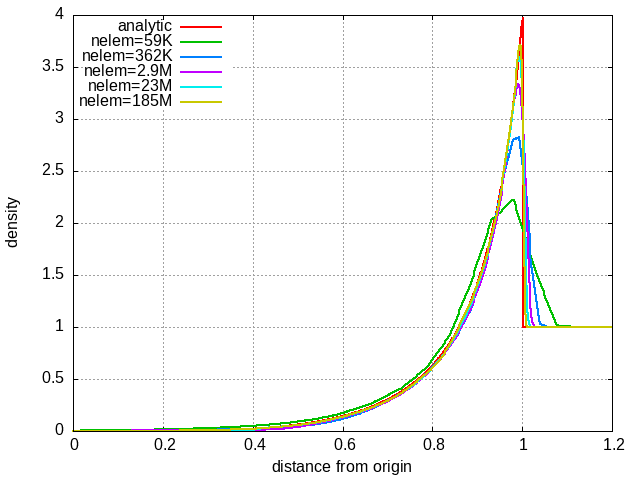
Convergence rate
The L1 error is computed as
where n is the number of points, and are the exact and computed solutions at mesh point v, and denotes the volume associated to mesh point v. The L1 error is depicted below for all meshes as a function of the average edge length. As expected, the error around the shock dominates, where the numerical method is only first order accurate.
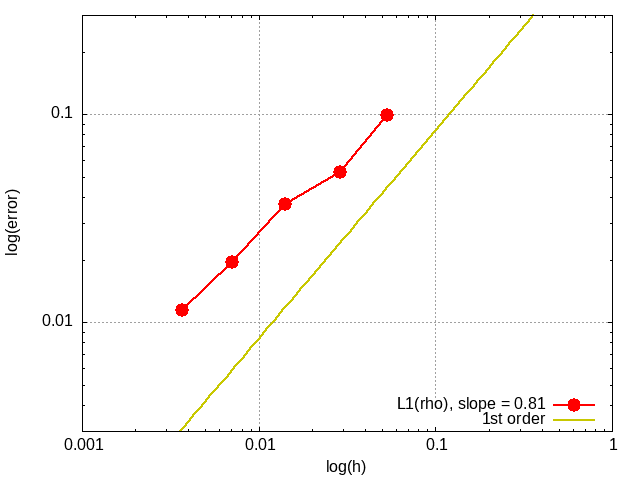
References
- L.I. Sedov, Similarity and Dimensional Methods in Mechanics, 10th ed. CRC Press. 1993.