V&V » RieCG: Slotted cylinder

This example uses RieCG in Inciter to compute a solid-body rotation problem. Such tests are frequently used to evaluate and compare numerical schemes for convection-dominated problems.

Here we evaluate the numerical method using Zalesak's slotted cylinder problem [1], augmented by Leveque [2] in order to examine the resolution of both smooth and discontinuous profiles.

Equations solved

In this example we numerically solve the linear advection equation coupled to the Euler equations, see also RieCG. as

\[ \begin{split} \frac{\partial U}{\partial t} + \frac{\partial F_j}{\partial x_j} = S,\qquad U = \begin{Bmatrix} \rho \\ \rho u_i \\ \rho E \\ c \end{Bmatrix}, \enskip F_j = \begin{Bmatrix} \rho u_j \\ \rho u_iu_j + p\delta_{ij} \\ u_j(\rho E + p) \\ u_j c \end{Bmatrix}, \enskip S = \begin{Bmatrix} S_\rho \\ S_{u,i} \\ S_E \\ S_c \end{Bmatrix}, \end{split} \]

where the summation convention on repeated indices has been applied, $\rho$ is the density, $u_i$ is the velocity vector, $E=u_iu_i/2+e$ is the specific total energy, $e$ is the specific internal energy, and $p$ is the pressure. $S_\rho$ , $S_{u,i}$ , $S_E$ , and $S_c$ are source terms that arise from the application of the method of manufactured solutions, used for verification only; these source terms are zero when computing practical engineering problems. The system is closed with the ideal gas law equation of state

\[ \begin{split} p = \rho e (\gamma - 1), \end{split} \]

where $\gamma$ is the ratio of specific heats.

Problem setup

The inital configuration for the scalar field, c, is depicted in the figure below.

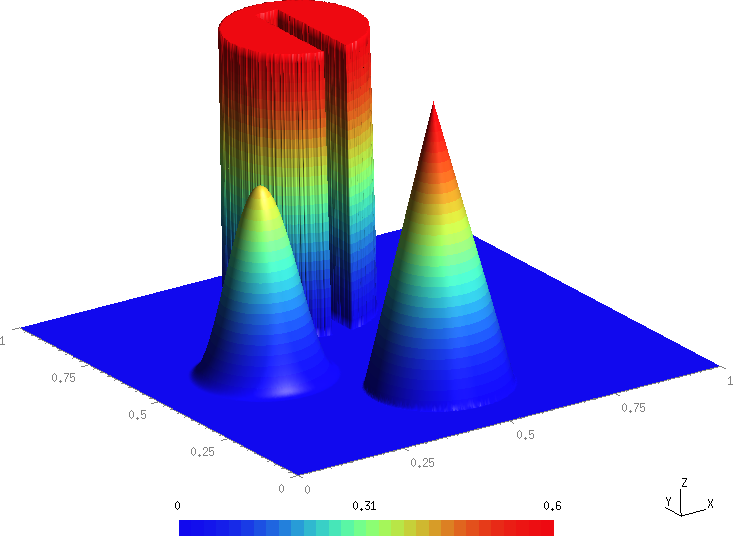
Image

While this is a 2D test problem, we calculate it on a 3D domain with the extents {0,1,0} x {0,1,0.05}, Since we are only interested in the evolution of the scalar, we prescribe the source terms that yield a stationary flow with a prescribed rotational velocity field ui = { 1/2 - y, x - 1/2, 0 } as

\[ \begin{split} S_\rho &= 0 \\ S_{u,i}&= \left\{ -\rho u_2, \rho u_1, 0 \right\} \\ S_E &= u_iS_{u,i} = 0 \\ S_c &= 0 \end{split} \]

Each solid body lies within a radius r0 = 0.15 centered at a point {x0,y0,0}. In the rest of the domain the solution is initially zero. The shapes of the three bodies can be expressed in terms of the normalized distance function for the respective reference point {x0,y0,0}

\[ \begin{split} r(x,y)=\frac{1}{r_0}\sqrt{(x-x_0)^2+(y-y_0)^2}. \end{split} \]

The center of the slotted cylinder is located at {x0,y0,0} = {0.5,0.75,0} and its geometry is given by

\[ \begin{split} c(x,y)=\left\{ \begin{aligned} &0.6\enskip\mathrm{if}\enskip|x-x_0|\ge0.025\enskip\mathrm{or}\enskip y\ge0.85,\\&0\enskip\mathrm{otherwise.} \end{aligned} \right. \end{split} \]

The corresponding analytical expression for the conical body is

\[ \begin{split} c(x,y)=0.6[1-r(x,y)],\quad(x_0,y_0)=(0.5,0.25), \end{split} \]

while the shape and location of the hump reads

\[ \begin{split} c(x,y)=0.2\left[1+\cos{\left(\pi\min\left(r(x,y),1\right)\right)}\right],\quad(x_0,y_0)=(0.25,0.5). \end{split} \]

The initial conditions are sampled from the analytic solutions above. We set inhomogeneous Dirichlet boundary conditions for the flow variables on all sides of the domain, sampling their analytic solutions. For the scalar, homogeneous Dirichlet conditions are set on those sides with normals in the x and y directions.

Code revision to reproduce

To reproduce the results below, use code revision 110c5cd and the control file below.

Control file

# vim: filetype=lua:

print "Scalar transport: slotted cylinder, cone, hump"

term = math.pi
ttyi = 100
cfl = 0.05

solver = "riecg"

part = "rcb"

problem = {
  name = "slot_cyl"
}

mat = { spec_heat_ratio = 5/3 }

bc_dir = {
  { 1, 1, 1, 1, 1, 1, 1 },
  { 2, 1, 1, 1, 1, 1, 1 },
  { 3, 1, 1, 1, 1, 1, 1 },
  { 4, 1, 1, 1, 1, 1, 0 },
  { 5, 1, 1, 1, 1, 1, 1 },
  { 6, 1, 1, 1, 1, 1, 0 }
}

fieldout = {
  iter = 1000
}

diag = {
  iter = 10,
  format = "scientific",
  precision = 12
}

Run using on 32 CPUs

./charmrun +p32 Main/inciter -i unitsquare_01_1.9M.exo -c slot_cyl.q

Visualization

ParaView can be used for interactive visualization of the numerically computed fields as

paraview out.e-s.0.32.0

Results

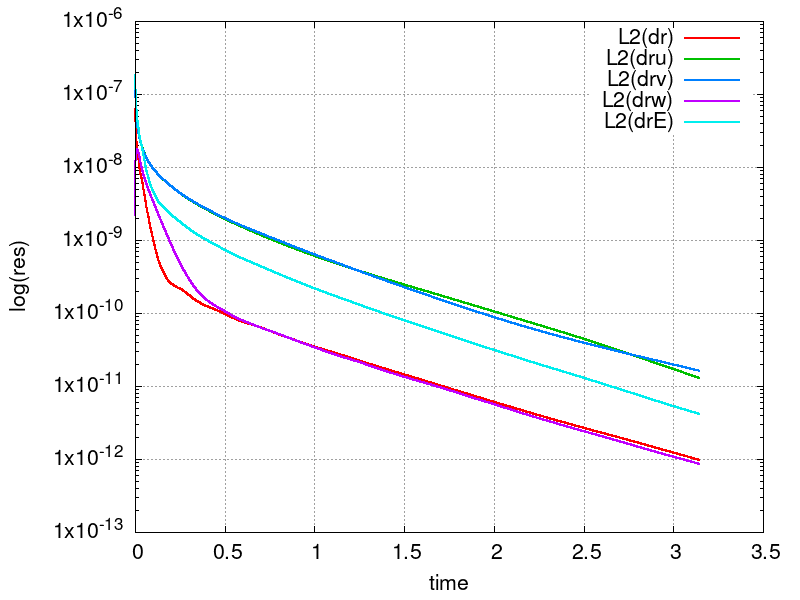
First, we verify that the flow variables are indeed constant in time. This verifies that that correct source terms have been chosen and that they have been implemented correctly. The following figure depicts the time evolution of L2-norm of the conserved flow variables.

Image

Gnuplot commands to reproduce the above plot:

set terminal png size 800,600 enhanced font "Helvetica,16"
set output "slotcyl_res.png"
set xlabel "time"
set ylabel "log(res)"
set logscale y
set grid
plot "diag" u 2:10 w l lw 2 t "L2(dr)", "" u 2:11 w l lw 2 t "L2(dru)", "" u 2:12 w l lw 2 t "L2(drv)", "" u 2:13 w l lw 2 t "L2(drw)", "" u 2:14 w l lw 2 t "L2(drE)"

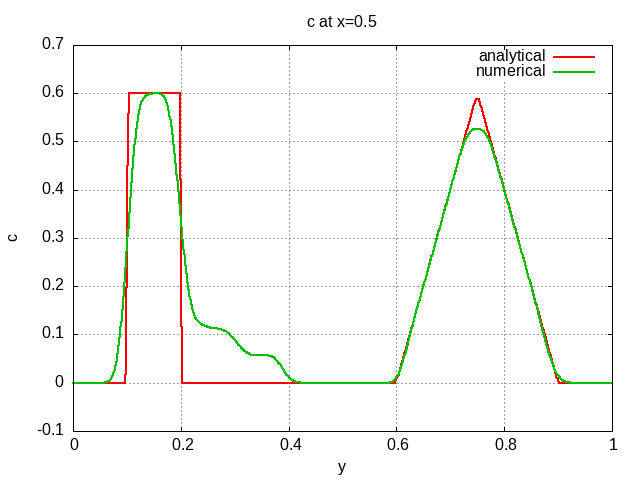
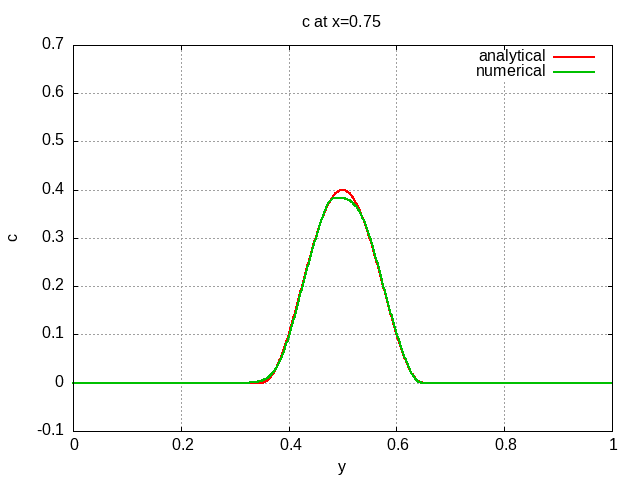
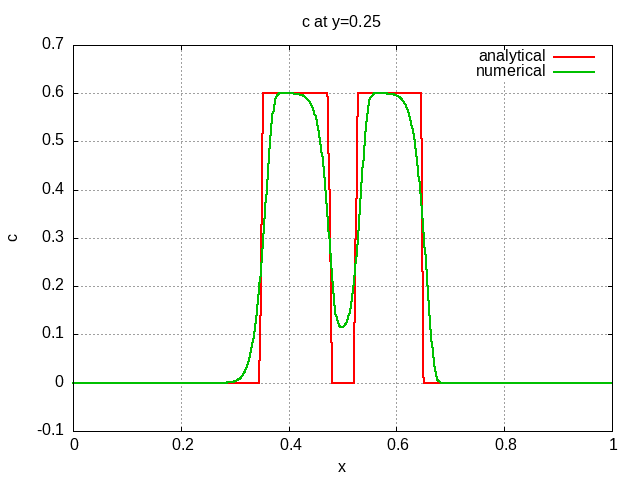
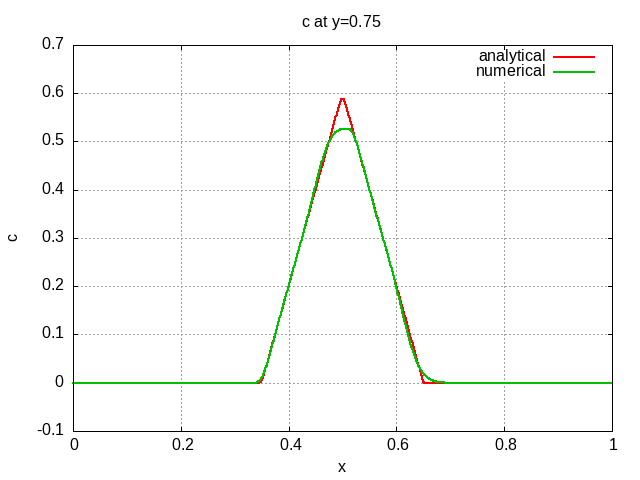
The scalar field after half revolution is depicted below with several line-outs at various locations so the solution can be compared to the analytic solution.

Image Image Image Image

References

[1] S.T. Zalesak, Fully multidimensional flux-corrected transport algorithms for fluids, J. Comput. Phys. 31,3, p.335-362, 1979.
[2] R.J. Leveque, High-resolution conservative algorithms for advection in incompressible flow, SIAM J. on Numerical Analysis, 33, p.627-665 1996.