RieCG computational performance

Strong scaling of computation

Using increasing number of compute cores with the same problem measures strong scaling, characteristic of the algorithm and its parallel implementation. Strong scalability helps answer questions, such as How much faster one can obtain a given result (at a given level of numerical error) if larger computational resources were available. To measure strong scaling we ran the Taylor-Green problem using a 794M-cell and a 144M-cell mesh on varying number of CPUs for a few time steps and measured the average wall-clock time it takes to advance a single time step. The figure below depicts timings measured on two different machines for both meshes, MeluXina and LUMI.

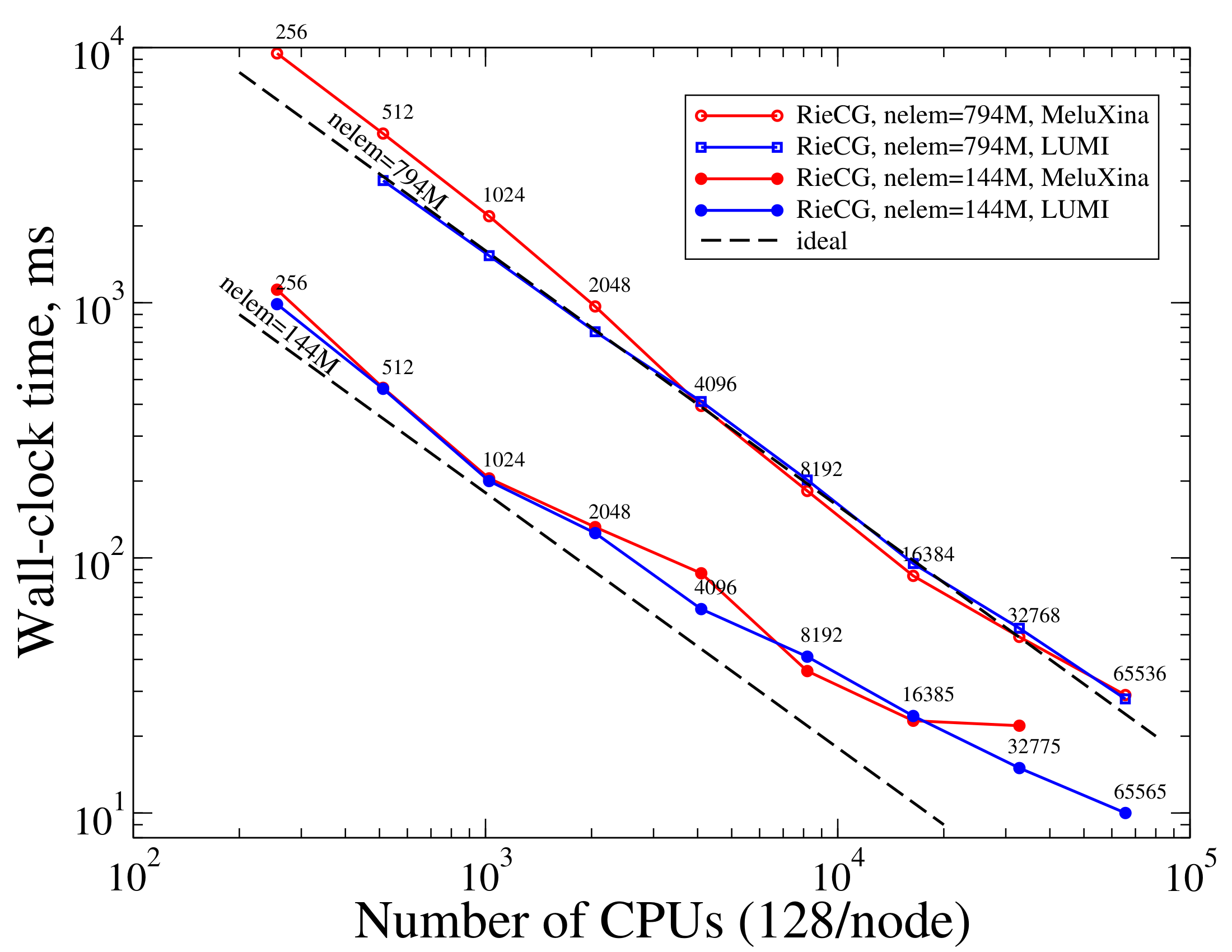
The figure shows that strong scaling of the RieCG solver is ideal with the larger mesh (794M tetrahedra) well into the range of O(10^4) CPU cores. The figure also shows that using the smaller work-load of 144M cells strong scaling is ideal at and below 1024 CPUs. Strong scaling is not ideal above 1024 CPUs with the smaller mesh, indicated by a nonzero angle between the ideal and the blue line with filled blue dots (144M on the LUMI machine). The data also shows that though non-ideal above 1024 CPUs, parallelism is still effective in reducing CPU time with increasing compute resources. Even at the largest run with 65,536 CPUs, which correspond to 2,209 tetrahedra and 642 mesh nodes per compute core on average, time-to-solution still largely decreases with increasing resources.

As usual with strong scaling, as more processors are used with the same-size problem, communication will eventually overwhelm useful computation and the simulation does not get any faster with more resources. The above figure shows that this point has not yet been reached at approximately 65K CPUs for neither of these two mesh sizes on these machines. The point of diminishing returns is determined by the scalability of the algorithm, its implementation, the problem size, the efficiency of the underlying runtime system, the hardware (e.g., the network interconnect), and their configuration.

Strong scaling of computation – second series

Approximately 17 months after the above data, the same benchmark series has been rerun on the same machine, using the same code computing the same problem using the same software configuration. The results are depicted below.

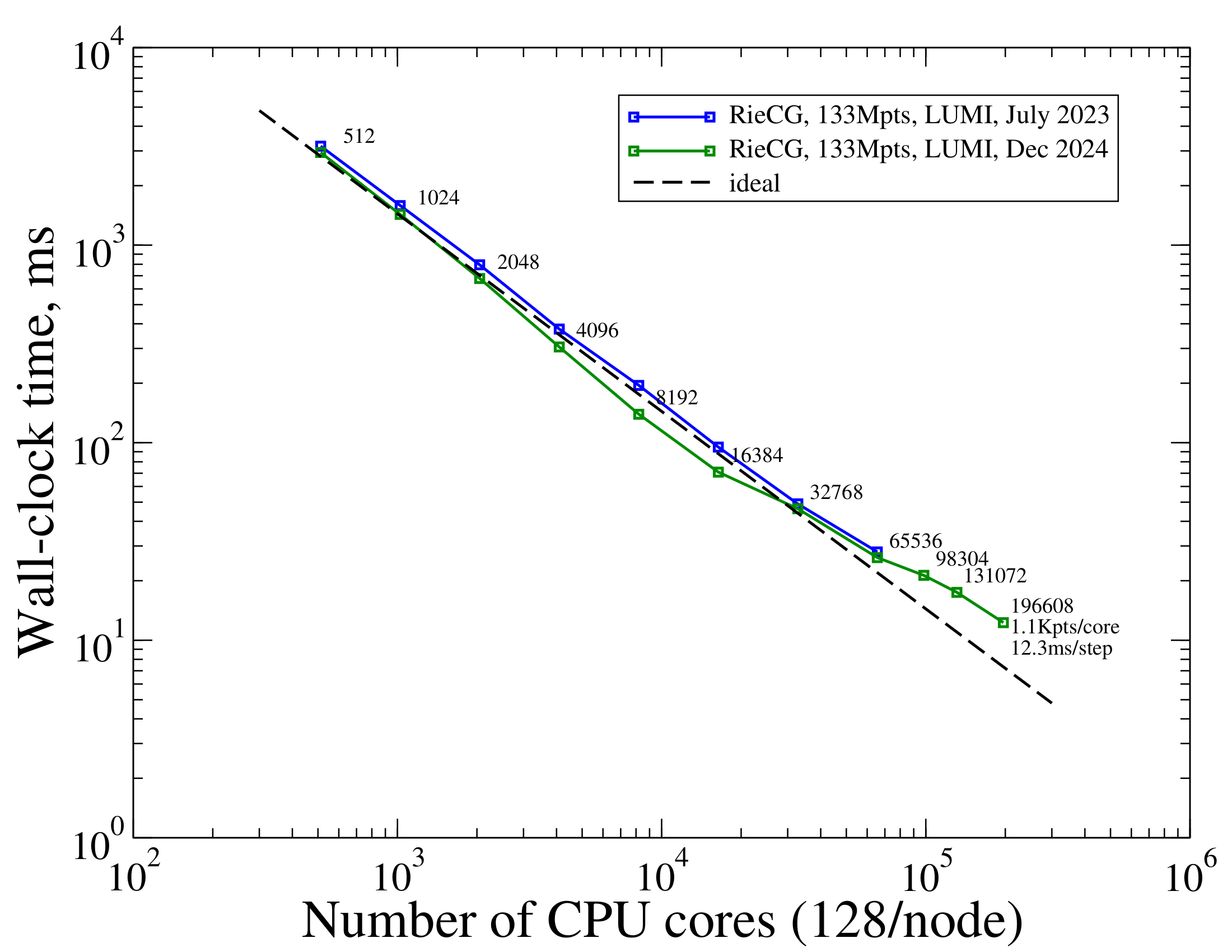
This figure shows that though strong scaling is not ideal, using larger number of CPUs still significantly improves runtimes up to and including the largest run employing 196,608 CPU cores. Considering the mesh with 794,029,446 tetrahedra connecting 133,375,577 points, this corresponds to approximately 1K mesh points per CPU core on average. Advancing a single (3-stage) time step takes 12 milliseconds of wall-clock time on average.

Comparing the two series using the larger mesh (nelem=794M, npoin=133M) also reveals some differerence. This could be due to different configurations of hardware, operating system, the network interconnect and/or it could also be due to different background loads between the two series.

Strong scaling of mesh read

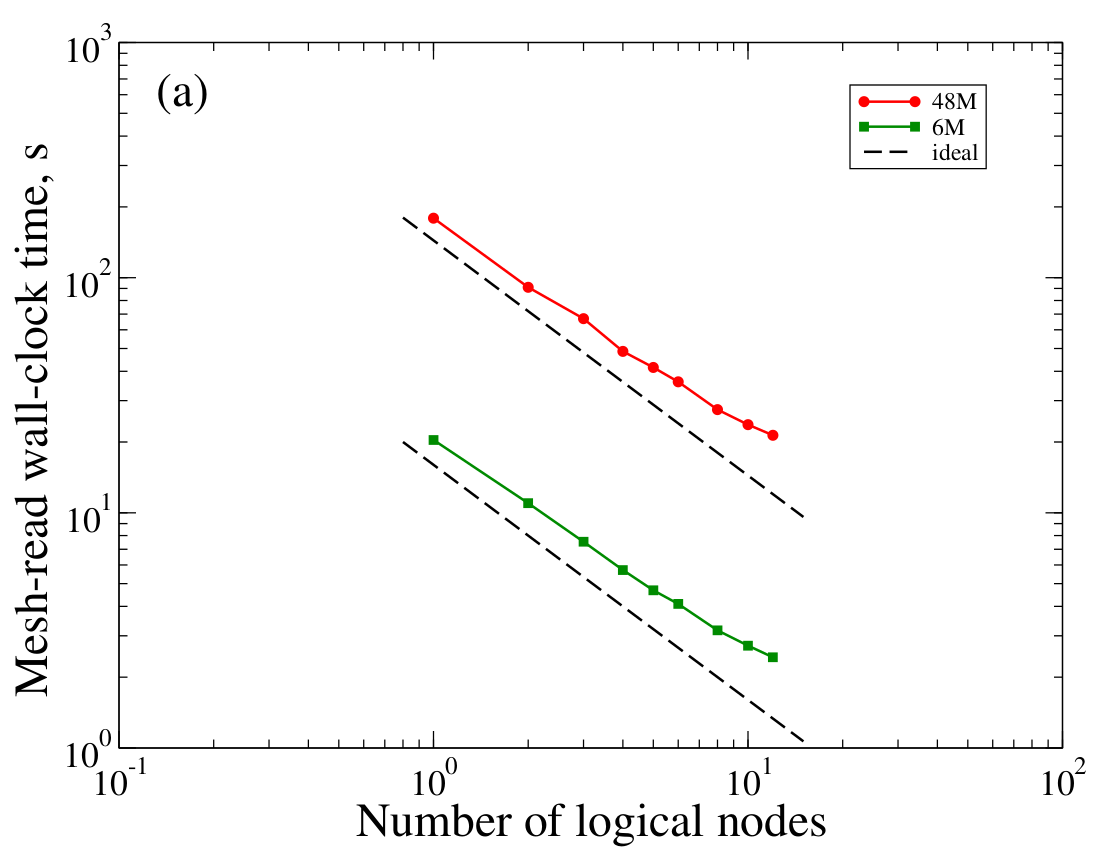
Xyst outsources the input and output from and to files of the computational mesh and field-data to the ExodusII library. ExodusII relies on the NetCDF (or optionally the HDF5) binary data formats, which facilitate out-of-order parallel reads and have been widely used in research and production for large scientific data in many fields. Xyst reads the computational mesh from a single ExodusII file in parallel and therefore this operation automatically benefits from available parallel hardware.

The figure below depicts strong scalability of reading the mesh in parallel. These timings were performed on a 12-node cluster in Charm++'s SMP mode. On this machine each compute node contains 32 CPU cores but using Charm++'s SMP mode the mesh-read was configured with one stream per compute node in parallel. One can see that scalability is good for both mesh sizes at all node counts.

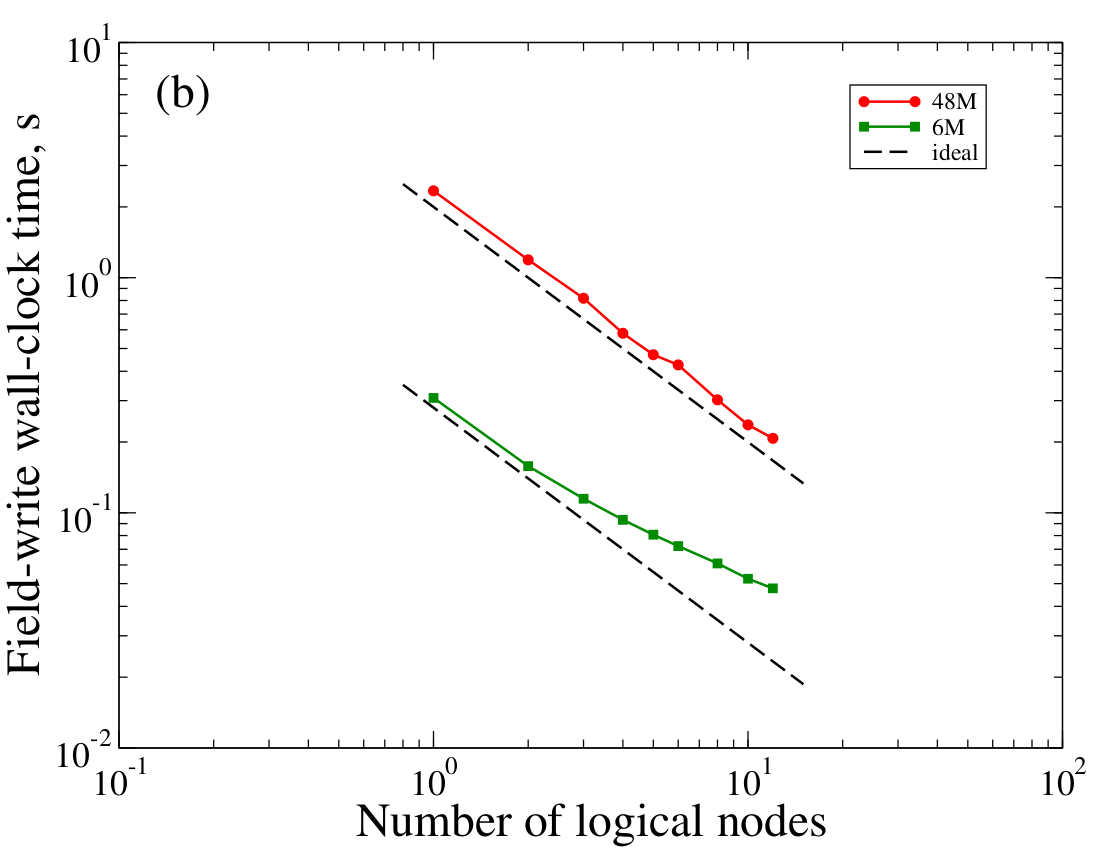
Strong scaling of field write

Writing large-field data (computed physics quantities associated to mesh nodes or elements) also uses the ExodusII library file format and software library. A different file is written for each mesh partition numbered so they can be automatically combined in memory by the visualization software, ParaView. In Xyst every parallel thread of execution writes data into one or more files and each file is appended data after new time steps with a user-configured frequency. Without overdecomposition each thread writes a single file. With overdecomposition each thread writes multiple files sequentially to ensure thread-safety of the MPI I/O calls underlying the ExodusII library. Charm++'s SMP mode can be configured so that each logical node writes multiple files sequentially. Since the number of logical nodes need not equal the number of compute threads, SMP mode is flexible enough to optimize I/O performance as the number of CPUs can be decoupled from the number of parallel writes.

The figure below depicts timings of writing the field output, physics variables computed in mesh nodes, appended to ExodusII files in parallel as time-stepping progresses. It is clear that for large data the strong-scalability of the writes is close to ideal.