ChoCG computational performance

Strong scaling of computation

Using increasing number of compute cores with the same problem measures strong scaling, characteristic of the algorithm and its parallel implementation. Strong scalability helps answer questions, such as How much faster one can obtain a given result (at a given level of numerical error) if larger computational resources were available. To measure strong scaling we ran the Lid-driven cavity using a 794M-cell mesh (133M points) on varying number of CPUs for a few time steps and measured the average wall-clock time it takes to advance a single time step. The figure below depicts timings measured on the LUMI computer.

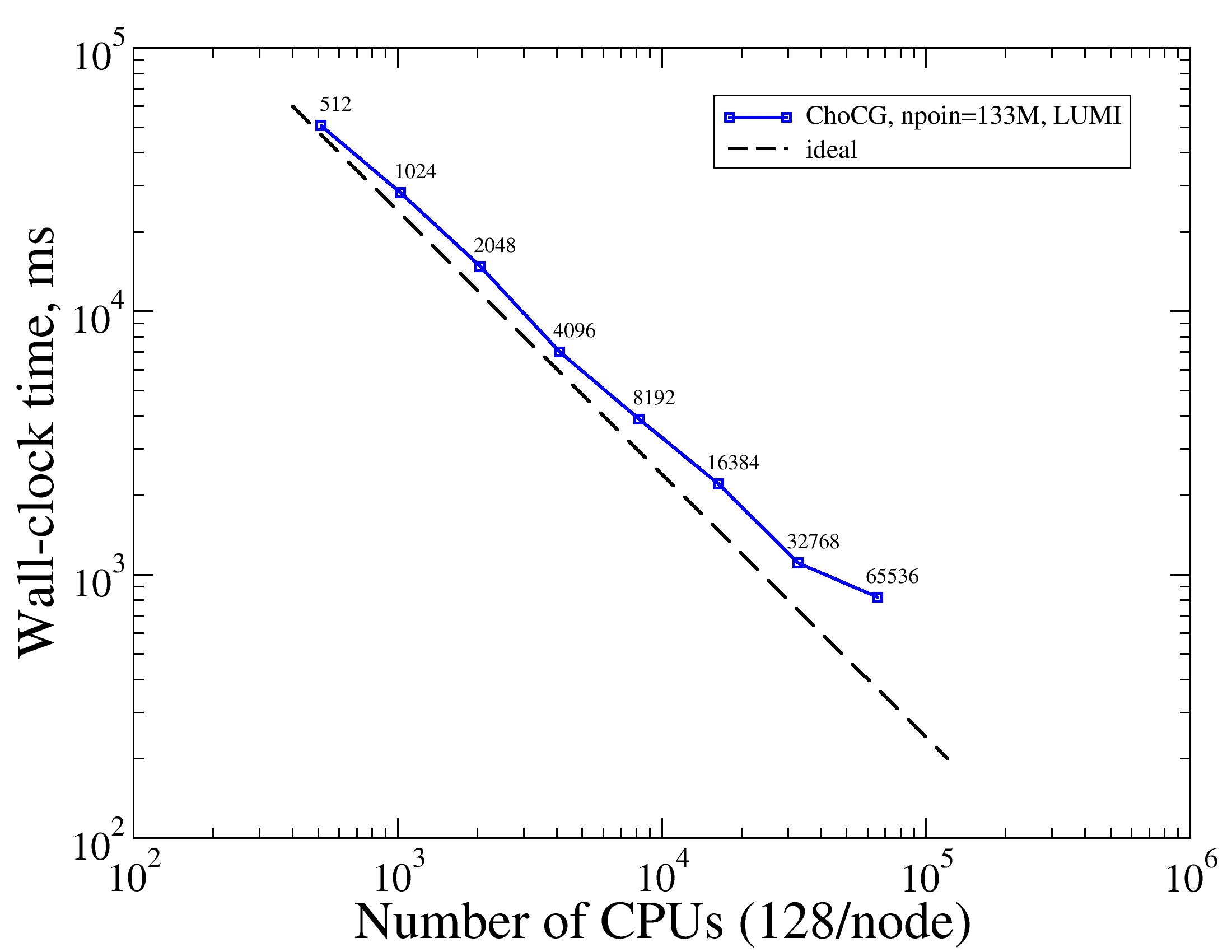
The figure shows that the ChoCG solver, while not ideal, scales well into the range of O(10^4) CPU cores. In particular, the figure shows that strong scaling is close to ideal at and below 32K CPUs. The departure from ideal is indicated by nonzero angles between the ideal and the blue line. The data also shows that though non-ideal above these points, parallelism is still effective in reducing CPU time with increasing compute resources. Even at the largest runs time-to-solution still largely decreases with increasing resources.

As usual with strong scaling, as more processors are used with the same-size problem, communication will eventually overwhelm useful computation and the simulation does not get any faster with more resources. The above figure shows that this point has not yet been reached at approximately 65K CPUs for this mesh on this machine. The point of diminishing returns is determined by the scalability of the algorithm, its implementation, the problem size, the efficiency of the underlying runtime system, the hardware (e.g., the network interconnect), and their configuration.