RieCG: Irregular Sedov blast with load balancing
This example uses RieCG in Inciter to induce parallel load imbalance and uses Charm++ to homogenize heterogeneous, dynamics, and unpredictable computational load speeding up the simulation by an order of magnitude. See also Papers.
With respect to solving partial differential equations on meshes, there is no magic using Charm++ compared to the message passing interface (MPI): the computational domain is still decomposed and communication of partition-boundary data still needs to be explicitly coded and communicated. However, an important difference compared to the usual divide-and-conquer strategy of domain-decomposition is that Charm++ also allows combining this data-parallelism with task parallelism. As a result, various tasks (e.g., computation and communication) can be performed independently and may be overlapped due to Charm++'s asynchronous-by-default paradigm. For an example of how task-parallelism can be specified in Charm++ with a different Euler solver, see [1].
Another unique feature of Charm++ compared to MPI is built-in automatic load-balancing. Charm++ can perform real-time CPU load measurement and if necessary can migrate data to under-loaded processors to homogenize computational load. This can be beneficial independent of its origin: adaptive mesh refinement, complex local equations of state, CPU frequency scaling or simply if some work-units have different number of boundary conditions (e.g., on a larger surface area) to apply compared to others. Multiple load balancing strategies are available in Charm++ and using them requires no extra programming effort: the feature is turned on by a command-line switch. Load balancing costs are negligible (compared to the physics operators) and can be beneficial for irregular work-loads at any problem size from laptop [2] to cluster [1].
The Sedov problem
We computed the Sedov problem [3], widely used in shock hydrodynamics to test the ability of numerical methods to maintain symmetry. In this problem, a source of energy is defined to produce a shock in a single computational cell at the origin at t=0. The solution is a spherically spreading wave starting from a single point. We used a domain that is eighth of a sphere with the mesh consisting of 23,191,232 tetrahedra and 3,956,135 points. See also RieCG: Sedov blast.
A modified Sedov problem
To exercise Charm++'s built-in load balancing, we modified the Sedov problem by adding extra computational load to the function that computes the pressure based on density and internal energy: if fluid density > 2.0 then sleep(1ms). This increases the cost of the equation of state evaluation whose location propagates in space and time, which induces load imbalance across multiple mesh partitions in parallel.
The images below depict the Spatial distributions of the extra load, corresponding to the fluid density exceeding the value 2.0, during time evolution of the Sedov solution: shortly after the onset of load imbalance and at a later time. As the computational domain decomposed into multiple partitions, worked on by different compute cores and nodes, the parallel load becomes inhomogeneous and work units must all wait for the slowest one.
Code revision to reproduce
To reproduce the results below, use code revision fadd412, the following patch
diff --git a/src/Physics/EOS.hpp b/src/Physics/EOS.hpp index e697caf..8403cb6 100644 --- a/src/Physics/EOS.hpp +++ b/src/Physics/EOS.hpp @@ -10,6 +10,8 @@ // ***************************************************************************** #pragma once +#include <thread> + #include "InciterConfig.hpp" namespace inciter { @@ -29,6 +31,8 @@ using inciter::g_cfg; inline double pressure( double r, double e ) { auto g = g_cfg.get< tag::mat_spec_heat_ratio >(); + using namespace std::chrono_literals; + if (r > 2.0) std::this_thread::sleep_for( 1ms ); return r * e * (g-1.0); }
by saving the above patch to file "p" and applying it as
patch -p1 -i p
Then use the control file below.
Control file
-- vim: filetype=lua: print "Sedov blast wave" nstep = 500 ttyi = 1 cfl = 0.5 part = "rcb" problem = { name = "sedov", -- p0 = 4.86e+3 -- sedov_coarse.exo -- p0 = 3.63e+4 -- sedov00.exo -- p0 = 2.32e+5 -- sedov01.exo p0 = 1.85e+6 -- sedov02.exo -- p0 = 14773333.33333 -- sedov02.exo+t0ref:u } mat = { spec_heat_ratio = 5/3 } bc_sym = { sideset = { 1, 2, 3 } } --href = { -- t0 = true, -- init = { "uniform" } --} diag = { iter = 1000, format = "scientific" } fieldout = { iter = 1000 }
Run on 32 CPUs
# no extra load: run without applying the patch above ./charmrun +p32 Main/inciter -i sedov02.exo -c sedov.q -b -l 1000 # extra load, no lb: apply the patch above, and run with ./charmrun +p32 Main/inciter -i sedov02.exo -c sedov.q -b -l 1000 # extra load, lb: apply the patch above, and run with ./charmrun +p32 Main/inciter -i sedov02.exo -c sedov.q -b -u 0.995 -l 20 +balancer MetisLB +balancer GreedyRefineLB
In the last command line above, we apply overdecomposition with -u 0.995, yielding 6399 mesh partitions on 32 CPUs, and turn on load balancing in Charm++ to use the MetisLB strategy in the first load balancing step and GreedyRefine subsequently. The -l 20 command line argument tells Charm++ to perform load balancing every 20th time step. Consult the Charm++ manual for details on load balancing.
Timings on a single workstation
The figure and table below show the effect of load balancing on wall-clock time: in this particular case the extra load would make the simulation about 36x more expensive, which load balancing speeds up by 6.1x.
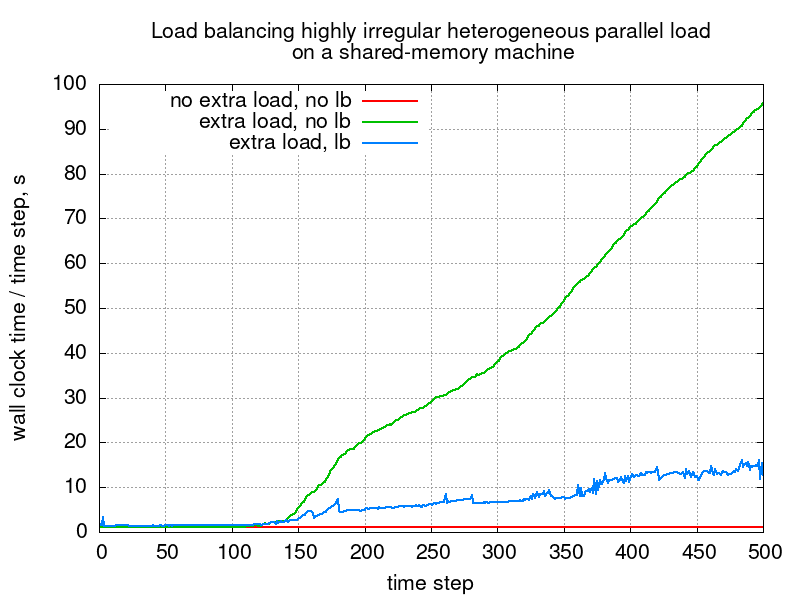
Measured wall-clock time of each time step during the Sedov calculation without extra load, as well as with extra load without and with load balancing. The area below each curve is proportional to the total computational cost.
Timings for the Sedov problem with and without load balancing on a single (shared-memory) workstation.
| Case | Extra load | Total time, s | Speed-up |
|---|---|---|---|
| 0 | no | 600 | - |
| 1 | yes | 17,310 | 1.0x |
| 2 | yes | 3,358 | 5.2x |
Run on multiple compute nodes
The following command line can be used to run the problem on a cluster of networked compute nodes each containing 32 CPU cores. Other than building Charm++ in SMP mode, no code changes are required.
# extra load, lb: apply the patch above, and run with ./charmrun +p $((31*$SLURM_NNODES)) Main/inciter -i sedov02.exo -c sedov.q +ppn 31 +pemap 1-31 +commap 0 -b -u 0.992 -l 20 +balancer DistributedLB
The above command line instructs the runtime system in SMP mode to execute on $SLURM_NNODES compute nodes. On each node it will assign 31 cores for computation and will designate 1 for communication only. Furthermore, Xyst will overdecompose the problem using a virtualization parameter of 0.992, which yields 30,962 mesh partitions assigned to the 248 compute cores. Such fine-grained work-units allow the runtime system to perform effective load balancing, which is invoked at every 20th time step.
Timings on a cluster
The following figure shows measured wall-clock times for each time step during computing the modified Sedov problem with and without extra load in SMP mode on 8 network-connected compute nodes. The area below each curve is proportional to the total computational cost of that simulation.
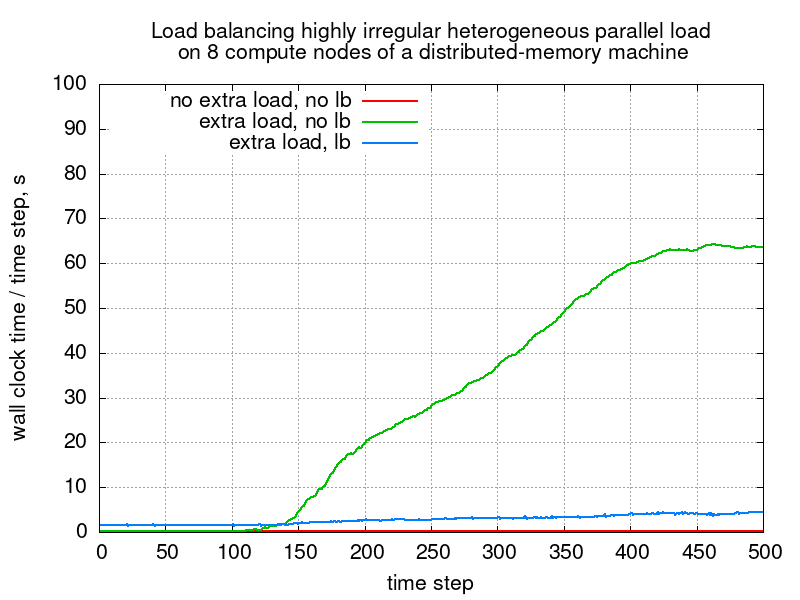
Timings for the Sedov problem with and without load balancing on 8 (network-connected, distributed-memory) compute nodes.
| Case | Extra load | Total time, s | Speed-up |
|---|---|---|---|
| no extra load | no | 108 | - |
| extra load, no LB | yes | 14,744 | 1.0x |
| extra load, LB | yes | 1,425 | 10.4x |
Summary
The above examples show that combining overdecomposition and Charm++'s automatic load balancing results in an order of magnitude reduction in wall-clock times for this particular irregular work-load. In this case the speed-up is about 6x on a single workstation and over 10x on multiple compute nodes.
References
- J. Bakosi, R. Bird, F.Gonzalez, C. Junghans, W. Li, H. Luo, A. Pandare, J. Waltz, Asynchronous distributed-memory task-parallel algorithm for compressible flows on unstructured 3D Eulerian grids, Advances in Engineering Software, 102962, 2021.
- W. Li, H. Luo, J. Bakosi, A p-adaptive Discontinuous Galerkin Method for Compressible Flows using Charm++, AIAA Scitech 2020 Forum, Orlando, Florida, 6–10 January, 2020.
- L.I. Sedov, Similarity and Dimensional Methods in Mechanics, 10th ed. CRC Press. 1993.